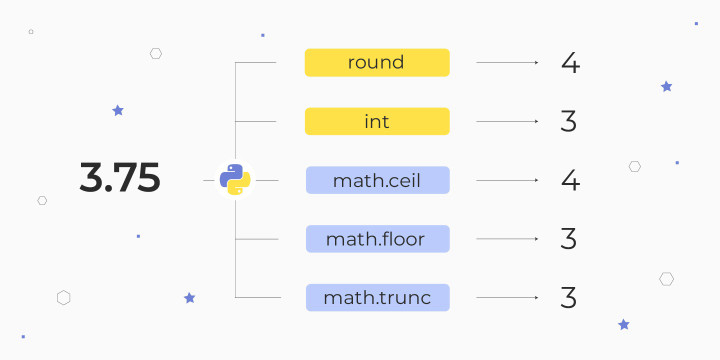
Округление в Python — round, int, модуль math
При выполнении ряда арифметических операций пользователю нужно следовать правилам округления. Преобразовывать нужно в большую или меньшую сторону, до целого значения или до сотых.
В Python для округления доступны функции round(), int() и модуль math. Последний дополнительно импортируется.
Встроенные функции
Для операции округления в Python есть встроенные функции — round() и int()
round
round(number, ndigits=None) — округляет число number до указанного количества знаков ndigits после запятой.
Это стандартная функция, которая для выполнения не требует подключения модуля math.
По умолчанию округление выполняется до ближайшего целого числа:
round(3.2) # 3
round(3.8) # 4Если указать второй аргумент ndigits, число будет округлено до нужного количества знаков после запятой:
round(3.14159, 2) # 3.14
round(3.14159, 3) # 3.142⚠️ Важно: поведение round() для чисел типа float иногда может казаться неожиданным. Например, round(2.675, 2) возвращает 2.67, хотя многие ожидают 2.68. Это не ошибка — причина в том, что большинство десятичных дробей нельзя точно представить в формате float.
from decimal import Decimal
print(Decimal.from_float(2.665))
> 2.6650000000000000355271...
print(Decimal.from_float(2.675))
> 2.674999999999999822364316... # в памяти 2.675 хранится как 2.67499...Проще говоря, Python округляет не то число, которое мы видим в коде, а то значение, которое реально хранится в памяти.
💭 Если нужна точная и предсказуемая работа с десятичными числами, лучше использовать Decimal. Подробнее об этом читайте в статье про Decimal и Fraction, в разделе "Округление".
int
int — встроенная функция, не требующая подключения дополнительных модулей. Её функция — преобразование действительных значений к целому путем округления в сторону нуля. Например:
int(5.9)
> 5
int(-5.77)
> -5Для положительных чисел функция int аналогична функции math.floor(), а для отрицательных — аналогично math.ceil(). Например:
import math
math.floor(3.999)
> 3
math.ceil(3.999)
> 4💡 Чтобы число по int преобразовать по математическим правилам, нужно выполнить следующие действия.
- Если число положительное, добавить к нему 0,5;
- Если число отрицательное, добавить -0,5.
Синтаксически преобразование оформляется так:
num = 5.77
int(num + (0.5 if num > 0 else -0.5))
> 6Функции из библиотеки Math
Модуль необходим в Python. Он предоставляет пользователю широкий функционал работы с числами. Для обработки алгоритмов сначала проводят импорт модуля.
import mathmath.ceil
Функция получила название от английского слова "ceiling" — "потолок"
Функция преобразовывает значение в большую сторону (вверх). Этот термин применяется и в математике. Он означает число, которое равно или больше заданного.
Любая дробь находится между двумя целыми числами. Например, 2.3 лежит между 2 и 3. Функция ceil() определяет большую сторону и возводит к нему результат преобразования. Например:
import math
math.ceil(3.25)
> 4Алгоритм определяет большую границу интервала с учетом знака:
import math
math.ceil(-3.25)
> -3math.floor
Функция получила название от английского слова "floor" — "пол"
math.floor() действует противоположно math.ceil() — округляет дробное значение до ближайшего целого, которое меньше или равно исходному. Округление происходит в меньшую сторону (вниз):
import math
math.floor(3.9)
> 3
math.floor(-2.1)
> -3При округлении учитывается знак перед данными.
math.trunc
Функция получила название от английского слова "truncate" — "урезать"
Функция характеризуется отбрасыванием дробной части. После преобразования получается целое значение без учета дроби. Такой алгоритм не является округлением в арифметическом смысле. В Пайтон просто игнорируется дробь независимо от ее значения:
import math
math.trunc(7.11)
> 7
math.trunc(-2.1)
-2💡 Избавиться от дроби можно без подключения модуля. Для этого есть стандартная функция int Она преобразовывает дробные числа в целые путем игнорирования дроби.
Различие округления в Python 2 и Python 3
В Python 2 и Python 3 реализованы разные принципы округления.
В Python 2 используется арифметическое округление. В нем наблюдается большое количество погрешностей, что приводит к неточностям в процессе вычислений.
Во втором Python есть только 4 цифры, которые ведут к преобразованию к меньшему значению — 1, 2, 3 и 4. Также 5 цифр, которые приводят к большему значению — 5, 6, 7, 8, 9. Такое неравное распределение ведет к тому, что погрешность постоянно нарастает.
Python 2 по правилам арифметического округления преобразует число 5,685 в 5,68 до второго знака. Такая погрешность связана с тем, что десятичные цифры float в двоичном коде невозможно корректно представить.
В Python 3 используются принципы банковского округления. Это означает, что преобразование производится к ближайшему четному. В таком случае также не удается полностью избежать возникающих ошибок, но программисты добиваются точности в подсчетах.
2,5 по правилам банковского преобразования будет равно 2, а 3,5 = 4 (значения возводятся к близкому четному). Минимизировать погрешности можно благодаря практически равной вероятности, что перед пятеркой будет четное или нечетное число.
Так и непонятно, как округлить число по правилу "если 5 - то в большую сторону)
*** Python 3.12.6 (tags/v3.12.6:a4a2d2b, Sep 6 2024, 20:11:23) [MSC v.1940 64 bit (AMD64)] on win32. ***
>>> round(123421.95, 1) 123421.9 >>> round(123421.85, 1) 123421.9 >>> round(123421.75, 1) 123421.8 >>> round(123421.65, 1) 123421.6 >>> round(123421.45, 1) 123421.4 >>> round(123421.35, 1) 123421.4 >>> round(123421.25, 1) 123421.2 >>> round(123421.15, 1) 123421.1 >>> round(123421.05, 1) 123421.1print(math.round(check_2 - chek_1, 1)) AttributeError: module 'math' has no attribute 'round'так будет работать:
print(round(check_2 - chek_1, 1))Мне нужно округлить данные об оперативной памяти, как это сделать?
system_ram = float(os_info.TotalVisibleMemorySize) / 1048576)"В Python 3 используются принципы банковского округления." - у нас в университете учили, что это огркгление по Гауссу
Банковское округление и округление по Гауссу — одно и то же, это округление к ближайшему четному числу.